Answer:
The answers are:
[-2.5,-2]
[1.5,2]
[2,2.5)
Explanation:
In order to determine when a function is decreasing, we have to know the rule. Given a
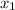 , the value of the function is
, the value of the function is
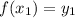 . Now we use other "x" value where
. Now we use other "x" value where
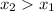 , if
, if
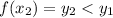 , we have:
, we have:
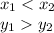
For any x that the condition is remained, the function is decreasing.
The "x" values that the function rever its sense (from down to up or from up to down), we can not considering in the interval ( we use the parentheses "(" or ")" )
So, according to the attached graph, the intervals where the function is decreasing are:
[-2.5,-2]
[1.5,2]
[2,2.5)