Answer:
a) 50 meters
b) 2354 meters
c) 12 seconds
d) 24.13 seconds
Explanation:
Hello!
a) How far is Lincoln above the ground when he shoots the gun?
We need to really understand what the variables represent in this question. Given that t is time, and h is height, the time at which he shoots the bullet will be 0, as the bullet hasn't started traveling yet. This means that we can solve for the original height of the bullet by plugging in 0 for time in the equation.
Equation:
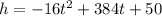
Plug in 0 for t:
The height at which Lincoln shot the bullet is 50 meters.
We can also look at this graphically. The height of origin will simply be when the x-value (in this case t-value) is 0. That means it is the point at which the graph intersects the y-axis, known as the y-intercept.
Standard form of a Parabola:
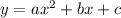
The y-intercept is the "c" value.
Given our equation:
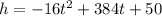
The c-value is 50. This proves that the y-intercept is 50.
b)How high does the bullet travel vertically relative to the ground?
We want to find the highest point of the graph. To do that, we can find the vertex.
We can utilize the Axis of Symmetry (AOS) to find the Vertex.
First, find the AOS using the formula:
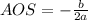
Plug it into the formula:
Plug in 12 for t in the equation:
Therefore, the highest point of the bullet is 2354 meters.
c)How long does it take the bullet to reach its greatest height?
We answered this in the last question. The t-value when h is at its highest is 12.
d)After how many seconds (round to nearest 100th) does the bullet hit the ground?
We have to solve for the values of t when h is 0 (when it touches the ground).
Set the equation to 0, and solve using the quadratic formula.
Quadratic formula:
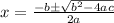
We are only going to take the positive solution, as we can't have a negative time. The solution that doesn't work is called an extraneous solution.
It takes approximately 24.13 seconds for the bullet to hit the ground.