Question

The area of a sector of a circle is represented by A=5/18πr to the power of 2, where r is the radius of the circle (in meters). What is the radius when the area is 40π square meters?


`40\pi = (5)/(18) \pi {r}^(2)`
​

Answer 1

r = 12

Explanation:

given

A =
`(5)/(18)` πr² and A = 40π

Equate the 2 areas and solve for r, that is

`(5)/(18)` πr² = 40π

Multiply both sides by 18 to eliminate the fraction

5πr² = 720π ( divide both sides by 5π )

r² =
`(720\pi )/(5\pi )` = 144

Take the square root of both sides

r =
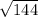`√(144)` = 12