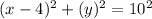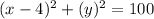Answer:
The equation of the circle is
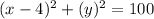
Explanation:
we know that
The general equation of the circle into center-radius form is equal to
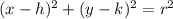
where
(h,k) is the center of the circle
In this problem
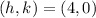
substitute
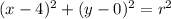
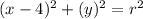
Find the radius
we know that
The distance between the points (-2,8) and (4,0) is equal to the radius
Applying the distance 's formula
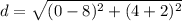
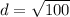
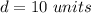
so
the radius is equal to
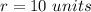
substitute