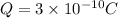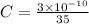Question

A. Calculate the electric potential energy stored in a capacitor that stores
`3.40 x 10^(-6)` C of charge at 24.0 V.

b. Two negative charges are held close to each other, and then released from rest. Write one or two sentences to describe the energy conversion that happens.

c. Calculate the capacitance of a system that stores
`3.0 x 10^(-10)` C of charge at 35.0 V.

Answer 1

a) E=1/2*QV=1/2*3.4*10^(-6)*24=4.08*10^(-5) J

b) They're negative, means that they'll repel. They have electrostatic energy. Then when released this energy converts into mechanical kinetic energy of motion.

c) C=Q/V=8.57*10^(-12) F, or 8.57 pF.

Answer 2

Part a)

As we know that energy stored inside the capacitor is given as

`U = (1)/(2)CV^2`

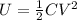
for a given capacitor we know

`Q = CV`

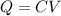
Now we can use it in above equation to find the energy

`U = (1)/(2)QV`

`U = (1)/(2)(3.4* 10^(-6))(24)`

`U = 40.8* 10^(-6) J`

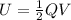
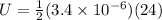
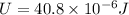
PART b)

If two negative charges are hold near to each other and then released

Then due to mutual repulsion they start moving away from each other

Due to mutual repulsion as the two charges moving away the electrostatic potential energy of two charges will convert into kinetic energy of the two charges.

So here as they move apart kinetic energy will increase while potential energy will decrease

Part c)

As we know that capacitance is given as

`C = (Q)/(V)`

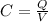
here we know that

`Q = 3* 10^(-10)C`

`V = 35 volts`

`C = (3* 10^(-10))/(35)`

`C = 8.6 * 10^(-12) F`