For this case, we propose a system of two equations with two unknowns.
Let:
x: Represents the number of children's tickets
y: Represents the number of adult tickets
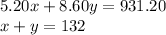
So, we clear x from the second equation:
x = 132-y
We replace in the first one.
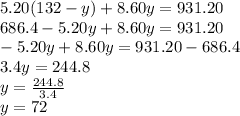
72 adult tickets were sold.
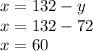
60 tickets for children were sold
Answer:
60 tickets for children
72 adult tickets