You can use the definition of the domain of a function and the fact that the logarithm function only accepts positive quantity.
The description that compares the domain of function A and function B correctly is given by:
Option B- the domain of function A is the set of real numbers is greater than 0
The domain of the function B is the set of real numbers greater than or equal to 1
What is the domain of a function?
Domain of a function is a set which contains all the values for which the function is defined and outputs well defined value.
How to find the domain of given functions?
Taking the first function:
Function A: f(x) = log(x)
log never takes in non positive quantity. Thus we need to have x > 0
log is defined for all positive values of x.
Thus, the input can be any positive real number.
Or,
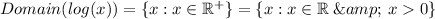
Taking the second function:
Function B: g(x) (plotted in given graph in question)
We can see that g(x) takes all values from x = 1 (it is between 0 and 2)
Assuming that the graph of g(x) keep being defined for rest of the values of x > 1, we get:
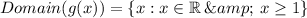
Thus, we have the correct description as:
Option B- the domain of function A is the set of real numbers is greater than 0
The domain of the function B is the set of real numbers greater than or equal to 1