Question

A 2m long rope is stretched between two supports with a tension that makes the speed of transverse waves 50m/s. What is the wavelength of the fundamental tone?

2m
6m
4m
8m

Answer 1

Answer: 4m

Step-by-step explanation:

In this situation, while the rope vibrates, a periodic wave travels through it, which is a standing wave.

In this sense, a standing wave has several harmonics and a fundamental tone (also called fundamental frequency), which is the lowest frequency of this periodic wave and is given by:

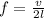`f=(v)/(2l)` (1)

Where:

`f` is the fundamental frequency

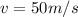`v=50 m/s` is the speed of the wave

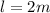`l=2 m` is the longitude of the rope

On the other hand, there is a relation between
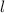`l` and the wavelength
`\lambda` of the fundamental tone:

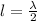`l=(\lambda)/(2)` (2)

Finding
`\lambda` from (2):

`\lambda=2l`

`\lambda=2(2 m)`

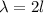
`\lambda=4 m` This is the wavelength of the fundamental tone