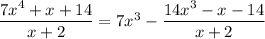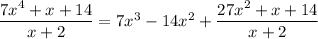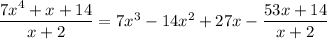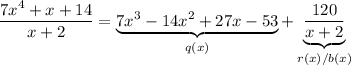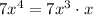 , and
, and
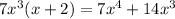 . Subtract this from the numerator and you get a remainder of
. Subtract this from the numerator and you get a remainder of
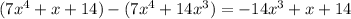
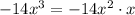 , and
, and
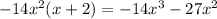 . Subtract this from the previous remainder and you get a new remainder of
. Subtract this from the previous remainder and you get a new remainder of
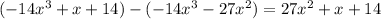
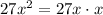 , and
, and
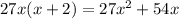 . Subtract this from the previous remainder and you get a new one of
. Subtract this from the previous remainder and you get a new one of
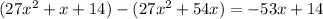
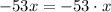 , and
, and
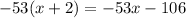 . Subtract this from the previous remainder and you get a new one of
. Subtract this from the previous remainder and you get a new one of
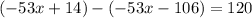
 doesn't divide 120, so we're done, and putting everything together we've shown that
doesn't divide 120, so we're done, and putting everything together we've shown that