Answer: The standard equation of this line is x-4y=8.
Explanation:
Since we have given that
Two coordinates are as follows:
(-4,-3) and (12,1)
So, slope would be
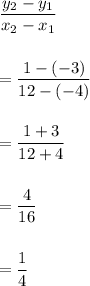
So, the standard form of equation of this line is given by

Hence, the standard equation of this line is x-4y=8.