Answer:
option (d) and (f) is correct.
The solution of given quadratic equation is 3 and -9.
Explanation:
Given quadratic equation
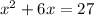
We have to solve the given quadratic equation using quadratic formula.
Consider
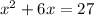 , we can rewrite it as
, we can rewrite it as
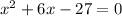
For the general quadratic equation
 the quadratic formula is given as
the quadratic formula is given as
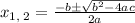
Here a = 1 , b= 6 and c = -27
Substitute, we get,
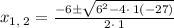
Solving further , we get,
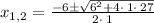
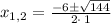
We know
 , we get,
, we get,
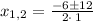
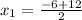 and
and
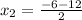
Solving we get,
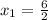 and
and
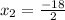
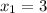 and
and

Thus, the solution of given quadratic equation is 3 and -9.
Thus, option (d) and (f) is correct.