Answer:
Hence, the limit of the function is:
1.5
Explanation:
We have to find a reasonable estimate of limit of the given expression:

Since on putting the limit x=-1 we observe that the numerator and denominator both are equal to zero i.e we get a 0/0 form.Hence, we will apply L'hospitals rule to find the limit of the function.
We will firstly differentiate the numerator and denominator to obtain the limit.
On differentiating numerator we get:
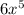
and on differentiating denominator we obtain:
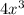
Hence, now we have to find the limit:
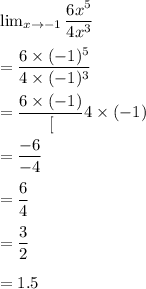
Hence, the limit of the function is:
1.5