Answer:
option (b) is correct.
The value of
 is 0.
is 0.
Explanation:
Given:
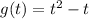 and
and
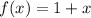
We have to find the value of

Consider the given function
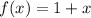
First evaluate value of function f(x) at x = 3 and 1 then substitute it in
 .
.
f(3) = 1 + 3 = 4
f(1) = 1 + 1 = 2
Substitute, we get
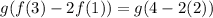
Solving further , we get,
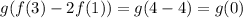
Now evaluate
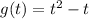 at t = 0 , we get,
at t = 0 , we get,
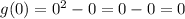
Thus, value of
 is 0.
is 0.
Thus, option (b) is correct.