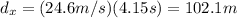Question

A man stands on the roof of a building of height 13.0and throws a rock with a velocity of magnitude 30.0 at an angle of 34.9 above the horizontal. You can ignore air resistance.(A) Calculate the maximum height above the roof reached by the rock.Take free fall acceleration to be 9.80(B) Calculate the magnitude of the velocity of the rock just before it strikes the ground.Take free fall acceleration to be 9.80(C) Calculate the horizontal distance from the base of the building to the point where the rock strikes the ground.Take free fall acceleration to be 9.80

Answer 1

(A) 28.1 m

The initial velocities of the rock along the x (horizontal) and y (vertical) directions are

`v_x = (30.0 m/s) cos 34.9^(\circ)=24.6 m/s\\v_y = (30.0 m/s) sin 34.9^(\circ) =17.2 m/s`

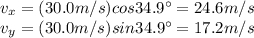
The vertical velocity of the rock at time t is given by

`v(t) = v_y -gt`

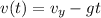
where
`v_y = 17.2 m/s` is the initial vertical velocity and
`g=9.8 m/s^2` is the gravitational acceleration.

At the point of maximum height, the vertical velocity is zero: v(t)=0, so we can calculate the time t at which this occurs:

`0=v_y -gt\\t=(v_y)/(g)=(17.2 m/s)/(9.8 m/s^2)=1.76 s`

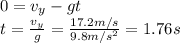
So, the rock has reached its maximum height after t=1.76 s. Now we can calculate its maximum height with the equation for the vertical position

`y(t) = y_0 + v_y t - (1)/(2)gt^2`

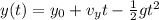
where
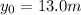`y_0 = 13.0 m` is the initial height. Substituting t=1.76 s, we find

`y_(max)=13.0 m + (17.2 m/s)(1.76 s)-(1)/(2)(9.8 m/s^2)(1.76 s)^2=28.1 m`

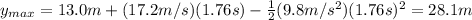
(B) 34.0 m/s

We need to find the time at which the rock hits the ground. We can do it by requiring y(t)=0 in the equation of the vertical position, so:

`0=y_0 + v_y t - (1)/(2)gt^2`

Substituting numbers, it becomes

`0=13+17.2 t -4.9t^2`

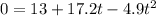
which gives two solutions:

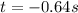`t=-0.64 s` (negative, so physically meaningless: we discard it)

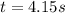`t=4.15 s` --> this is our solution, the time at which the rock hits the ground

Now we can substitute t=4.15 s in the equation of the vertical velocity, to find the vertical velocity of the rock as it strikes the ground:

`v_y(t)=v_0 -gt=17.2 m/s-(9.8 m/s^2)(4.15 s)=-23.5 m/s`

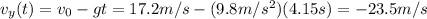
The negative sign only means the direction is downward. However, this is only the vertical component of the velocity: since the rock is also moving along the horizontal direction, with constant velocity
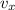`v_x`, the magnitude of the resultant velocity is

`v=√(v_x^2+v_y^2)=√((24.6 m/s)^2+(-23.5 m/s)^2)=34.0 m/s`

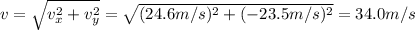
(C) 102.1 m

Since the rock is moving by uniform motion along the x-axis, the horizontal distance is simply given by:

`d_x = v_x t`

and substituting the total time of the fall, t=4.15 s, we find

`d_x = (24.6 m/s)(4.15 s)=102.1 m`