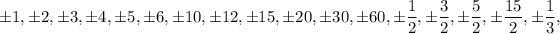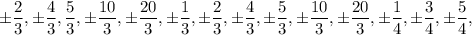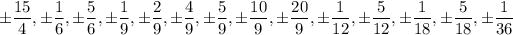Question

Which of the numbers below are some potential roots of p(x) 36x2 -7x-60 according to the rational root theorem?

Answer 1

This expression can not be factored with rational numbers.

The polynomial is not factor able with rational numbers.

Explanation:

Answer 2

`\pm 1,\pm 2,\pm 3,\pm 4,\pm 5,\pm 6,\pm 10,\pm 12,\pm 15,\pm 20,\pm 30,\pm 60,\pm (1)/(2),\pm (3)/(2),\pm (5)/(2),\pm (15)/(2),\pm (1)/(3),`

`\pm (2)/(3),\pm (4)/(3),(5)/(3),\pm (10)/(3),\pm (20)/(3),\pm (1)/(3),\pm (2)/(3),\pm (4)/(3),\pm (5)/(3),\pm (10)/(3),\pm (20)/(3),\pm (1)/(4),\pm (3)/(4),\pm (5)/(4),`

`\pm (15)/(4),\pm (1)/(6),\pm (5)/(6),\pm (1)/(9),\pm (2)/(9),\pm (4)/(9),\pm (5)/(9),\pm (10)/(9),\pm (20)/(9),\pm (1)/(12),\pm (5)/(12),\pm (1)/(18),\pm (5)/(18),\pm (1)/(36)`

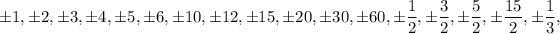
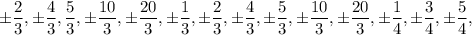
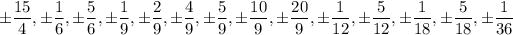
Explanation:

The given polynomial is

`p(x)=36x^2-7x-60`

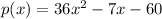
We need to find the potential roots of given polynomial according to the rational root theorem.

According to the rational root theorem, the potential roots are

`x=\pm (p)/(q)`

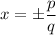
where, p is a factor of constant term and q is the factor of leading term.

In the given polynomial constant term is -60 and leading term 36.

Factors of 60 are ±1,±2,±3,±4,±5,±6,±10,±12,±15,±20,±30,±60.

Factors of 36 are ±1,±2,±3,±4,±6,±9,±12,±18,±36.

Now, the potential roots are

`\pm 1,\pm 2,\pm 3,\pm 4,\pm 5,\pm 6,\pm 10,\pm 12,\pm 15,\pm 20,\pm 30,\pm 60,\pm (1)/(2),\pm (3)/(2),\pm (5)/(2),\pm (15)/(2),\pm (1)/(3),`

`\pm (2)/(3),\pm (4)/(3),(5)/(3),\pm (10)/(3),\pm (20)/(3),\pm (1)/(3),\pm (2)/(3),\pm (4)/(3),\pm (5)/(3),\pm (10)/(3),\pm (20)/(3),\pm (1)/(4),\pm (3)/(4),\pm (5)/(4),`

`\pm (15)/(4),\pm (1)/(6),\pm (5)/(6),\pm (1)/(9),\pm (2)/(9),\pm (4)/(9),\pm (5)/(9),\pm (10)/(9),\pm (20)/(9),\pm (1)/(12),\pm (5)/(12),\pm (1)/(18),\pm (5)/(18),\pm (1)/(36)`