Answer:
28 whole soda cans or 28.4 soda cans (rounding to nearest tenth)
Explanation:
The soda cans and the pitcher can be modeled as cylinders.
Volume of a cylinder

where:
- r is the radius
- h is the height
Diameter of circle
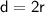
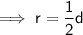
Volume of Soda can
Given values:
- d = 6.5 ⇒ r = 3.25 cm
- h = 12 cm
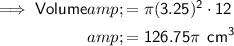
Volume of Pitcher
Given values:
- d = 20 ⇒ r = 10 cm
- h = 36 cm

To calculate how many cans of soda the pitcher will hold, divide the volume of the pitcher by the volume of one soda can:

Therefore, the pitcher can hold 28 soda cans (nearest whole can), or 28.4 soda cans (nearest tenth).