Question

an airplane propeller rotating at 1200 rpm has 2600 J of kinetic energy. what is its rotational inertia?​

Answer 1

Moment of Inertia:

`I = 0.33 \; \text{J} \cdot \text{kg} \cdot \text{m}^(2)`.

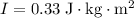Step-by-step explanation

The angular velocity is in rpm or rotations per minutes. In SI units, the unit should reads radians per second. Each rotation is
`2\pi` radians and there are sixty seconds in one minute. Convert to SI units:

`\omega = 1200 \; \text{RPM} * 2\pi * \frac{1\;\text{minute}}{60\;\text{s}} = 125.7 \;\text{s}^(-1)`.

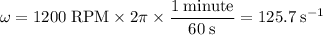"Radian" is implied and isn't shown in the unit.

`KE_\text{rotational} = (1)/(2) \;I \cdot \omega^(2)`.

`I = \frac{KE_\text{rotational}}{(1)/(2) \;\omega^(2)} = \frac{2\;KE_\text{rotational}}{\omega} = (2 * 2600)/(125.7^(2)) = 0.33 \;\text{kg}\cdot\text{m}^(2)`.