Answer: Yes, the approximate annual rate is 1.7%
Explanation:
Here, the principal amount, P = $ 83,
Time, t = 42 years
Amount after 42 years, A = $ 166
Let the annual rate of interest = r %,
By the compound interest formula,
We can write,
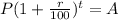




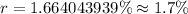
⇒ The annual rate of interest = 1.7% ( Approx )