PART A)
From gravitational force formula we know that
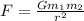
now we have
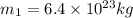

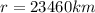
now we have
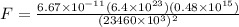
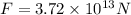
Part B)
again from same formula as we used above to find the force
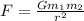
now we have
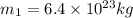
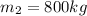

now we have

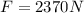
PART C)
here in circular orbit the speed of the satellite will remain the same always
So here kinetic energy of satellite will always remain same
There is no change in kinetic energy of satellite
Part d)
Since satellite is revolving in circular orbit so the distance will always remain the same
As well as the two masses is also constant
So here the gravitational force between them is always same and it will not change