Question

Find all solutions to the equation secx(2cosx-sqrt2)=0

Answer 1

Option A.

`x = (\pi)/(4) +2k\pi` and
`x = 7(\pi)/(4) +2k\pi`

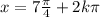
Explanation:

We have the following expression:

`secx(2cosx -√(2)) = 0`

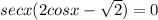
For this equation to fulfill any of the two terms, or both, they must be zero:

That is to say:

`secx = 0` or
`(2cosx -√(2)) = 0`

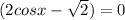
We know that
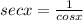`secx = (1)/(cosx)` is different from 0 for all x.

Then we only have one option left.

`(2cosx -√(2)) = 0`

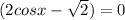
We clear x from the equation:

`2cosx = √(2)`

`cosx = (√(2))/(2)`

`x = acos((√(2))/(2))`

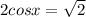
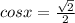
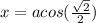
`x = (\pi)/(4) +2k\pi` and
`x = 7(\pi)/(4) +2k\pi`

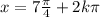
where k is an integer