Part A)
As we know that spring force is given by
F = kx
here x = stretch in the spring from natural length
So here when spring reaches to its natural length
Force due to spring = 0
so acceleration = 0
Part b)
When spring is compressed from its natural length it will have elastic potential energy in it
so it is given by

now we know that there is no friction in it so maximum kinetic energy of the launcher must be equal to the elastic potential energy of the spring
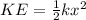
here we have
k = 70 N/m
x = 0.4 m
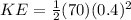
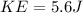
Part c)
Now to find the speed we know that
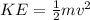
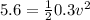

so its speed is 6.11 m/s