Question

The electric field between square the plates of a parallel-plate capacitor has magnitude E. The potential across the plates is maintained with constant voltage by a battery as they are pulled apart to twice their original separation, which is small compared to the dimensions of the plates. The magnitude of the electric field between the plates is now equal toa)E.b)E/4.c)E/2.d)4E.e)2E.

Answer 1

c) E/2

Step-by-step explanation:

The relationship between magnitude of electric field (E), distance between the plates (d) and voltage across the plates (V), for a uniform electric field, is given by:

`V=Ed`

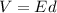
Re-arranging it, we can write it as

`E=(V)/(d)`

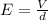
in the problem, the potential across the plates is kept constant: V' = V.

However, the distance between the plates is doubled: d' = 2d

Therefore, we can calculate the new magnitude of the electric field:

`E'=(V')/(d')=(V)/(2d)=(1)/(2)(V)/(d)=(E)/(2)`

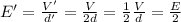
So the correct answer is

c)E/2