Answer:
The maximum monthly profit is 18050.
Step-by-step explanation:
The given function is

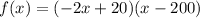
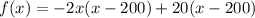
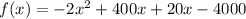
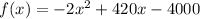 .... (1)
.... (1)
The vertex of a quadratic function
 ..... (2)
..... (2)
is defend as
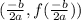
From (1) and (2) we get
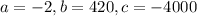
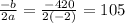
Put x=105 in the given function.
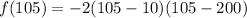
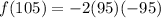

Therefore the maximum monthly profit is 18050.