Question

Michael’s weight can be represented by the expression 72x^5. Al’s weight can be represented by the expression 9x^7.

Answer 1

Part A) The ratio is
`(72x^(5))/(9x^(7))`

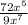
Part B)
`(8)/(x^(2))`

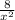
Part C)
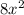`8x^(2)` ----> The answer change

Explanation:

Let

a------> Michael's weight

b----> Al's weight

we have

`a=72x^(5)`

`b=9x^(7)`

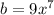
Part A) What is the ratio of Michael's weight to Al's weight

we know that

`ratio=(a)/(b)`

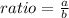
substitute the values

`ratio=(72x^(5))/(9x^(7))`

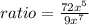
Part B) Simplify the ratio from part A)

we have

`ratio=(72x^(5))/(9x^(7))`

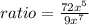
we know that

`(72)/(9)=8`

`(x^(5))/(x^(7))=(1)/(x^(2))`

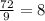
substitute

`ratio=(72x^(5))/(9x^(7))=(8)/(x^(2))`

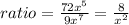
Part C) If the exponents in each expression were negative, instead of positive, would that change your answer for part b?

If the exponents in each expression were negative

then

the expression will be

`ratio=(72x^(-5))/(9x^(-7))`

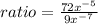
we know that

`(72)/(9)=8`

`(x^(-5))/(x^(-7))=(x^(7))/(x^(5))=x^(2)`

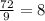
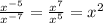
substitute

`ratio=(72x^(-5))/(9x^(-7))=8x^(2)`

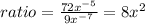
therefore

The answer change