Question

A quadrilateral has vertices (2,2), (2,-2), (-1,2), (-1,2) what special quadrilateral is formed by connecting the midpoint of the sides?

Answer 1

Rhombus.

Explanation:

Consider quadrilateral ABDC with vertices at points (2,2), (2,-2), (-1,2), (-1,-2). This quadrilateral is a rectangle. The sides' midpoints are:

• E(2,0);
• F(0.5,-2);
• G(-1,0);
• H(0.5,2).

Quadrilateral EFGH is always a parallelogram, because midlines EF and GH are parallel to the diagonal AD (by the triangle's midline theorem) and HE, GF are parallel to the diagonal BC. Thus, EF || GH and HE || GF.

Note that

`EF=FG=GH=HE=√((2+0.5)^2+(0+2)^2)=√(6.25+4)=√(10.25)\ un.`

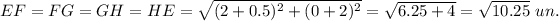
Thus, this parallelogram is rhombus.