Question

Bill forgets to put his car in park and it starts rolling west. When it is moving at a speed of 3.5 m/s, it collides with Tanya's car, which is moving at a speed of 2m/s east. Bill's car bounces backward (to the east) at a speed of 2 m/s. Bill's car has a mass of 900 kg, and Tanya's car has a mass of 1100 kg.

a. What is the total momentum of the system before collision?

b. What is the total momentum of the system after the collision?

c, What is the velocity of Tanya's car after the collision?

Answer 1

a) Simply add the momentum but remember that velocities in opposite directions have opposite signs. West direction is positive, east - negative.

p = 900*3.5 + 1100*(-2) = 950 kg*m/s.

b) After the collision (thanks to the law of conservation of momentum) the momentum is still 950 kg*m/s

c) Since the total momentum is the same (950), but something inside changed, write

950 = 900*(-2)+1100*u, so solve it

u=2.5 m/s. Positive sign means that Tanya's car goes west.

Regards,

226483

Answer 2

PART A)

momentum of Bill's car

mass = 900 kg

speed = 3.5 m/s towards west

so momentum of this car given as

`P_1 = 900(3.5) = 3150 kg m/s`

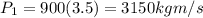
Similarly momentum of Tanya's car

mass = 1100 kg

speed = 2 m/s towards East

so momentum will be

`P_2 = 1100(2) = 2200 kg m/s`

Total momentum of both cars will be

`P = 3150 -2200 = 950 kg m/s` Towards west

PART B)

Since there is no external force on the system of two cars

So here total momentum of both cars will remains conserved

So final momentum of two cars will be same as initial momentum

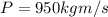`P = 950 kg m/s` towards west

Part C)

final momentum of Bills car

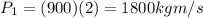`P_1 = (900)(2) = 1800 kg m/s` Towards East

now we have

`P_1 + P_2 = 950`

`1100 v - 1800 = 950`

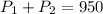
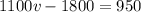
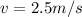`v = 2.5 m/s` towards west