Question

Given: △ABC, BK=10, AC=30, m∠NMO=90°, MN=MO, BK⊥AC, NO∥AC, M∈AC Find: NO

Answer 1

Answer: 12 unit.

Explanation:

Given : In triangle ABC,

m∠NMO=90°, MN=MO, BK⊥AC, NO∥AC, M∈AC, BK=10, AC=30,

We have to find : NO

Since, NO∥AC,

By the alternative interior angle theorem,

`\angle BNO\cong \angle BAC`

`\angle BON\cong \angle BCA`

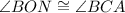
Also,

`\angle NBO\cong \angle ABC`

Thus, by AAA similarity postulate,

`\triangle NBO\cong \triangle ABC`

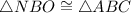
Let S ∈ NO such that BS ⊥ NO,

By the property of similar triangles,

`(BS)/(BK)=(NO)/(AC)`

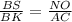
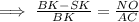`\implies (BK-SK)/(BK)=(NO)/(AC)` -------- (1),

Now, m∠NMO=90° and MN=MO,

Let J ∈ NO, such that MJ⊥NO

⇒ Triangle NMO is a isosceles triangle,

⇒ ∠MNJ = 45°,

`\implies tan 45^(\circ) = (MJ)/(NJ)`

`\implies MJ = NJ = SK`

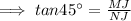
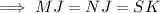
`\implies NO = 2 SK` -------(2)

From equation (1),

`\implies (BK-SK)/(BK)=(2 SK)/(AC)`

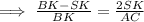
Since, BK=10, AC=30

`\implies (10-SK)/(10)=(2 SK)/(30)`

`\implies 300 - 30 SK = 20 SK \implies 50 SK = 300\implies SK = 6`

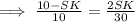
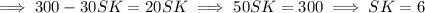
From equation (2),

NO = 2 × 6 = 12 unit.