Answer: The correct option is (B) (-2, 13).
Step-by-step explanation: We are given to find the solution of the following system of equations :

Multiplying equation (ii) by 3, we have
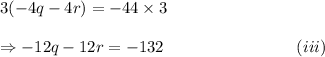
Adding equations (i) and (iii), we get
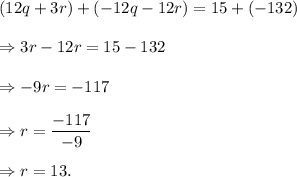
From equation (ii), we get
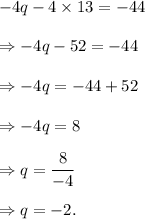
Thus, the required solution is (q, r) = (-2, 13).
Option (B) is CORRECT.