Answer : The value of
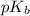 is, 10.8
is, 10.8
Explanation :
First we have to calculate the value of
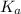 .
.
The expression used for the calculation of
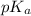 is:
is:
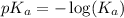
Now put the value of
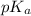 in this expression, we get:
in this expression, we get:
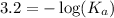
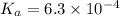
Now we have to calculate the value of
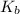 .
.
Formula used :
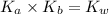
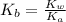
Now put the value of
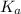 in this expression, we get:
in this expression, we get:
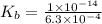

Now we have to calculate the value of
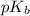 .
.
The expression used for the calculation of
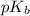 is:
is:
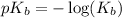
Now put the value of
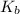 in this expression, we get:
in this expression, we get:
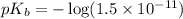

Therefore, the value of
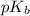 is, 10.8
is, 10.8