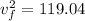Question

A diver of mass 101 kg jumps upward off a diving board and into the water. The diving board is 6 m above the water.

a. When the diver jumps, she has a speed of 1.2 m/s, How much kinetic energy does she have?

b How much gravitational potential energy will she have gained at her highest point? Explain how you found the answer.

c. Based on the diver's speed from part (a), how high above the board will she rise?

d. How fast will the diver be moving when she hits the water?

Answer 1

a) KE=1/2 mv^2=72.72 J

b) According to law of conservation of energy, PE=KE=72.72 J

c) mgh=KE, h=KE/mg=0.073 m

d) KE2=KE+mgh=72.72+101*9.8*6=6011.52 J

`v=√(2KE_2/m)= 10.91` m/s

Answer 2

PART a)

As we know that kinetic energy is given by

`K = (1)/(2) mv^2`

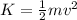
here we know that

m = 101 kg

v = 1.2 m/s

now from above equation

`K = (1)/(2)(101)(1.2)^2`

`K = 72.72 J`

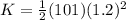
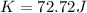
Part B)

As we know that gravitational potential energy is given by

`U = mgh`

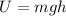
Now we know that here there is no loss in energy due to friction

So she will gain its potential energy by the loss of kinetic energy

So her gain in potential energy at the top = initial kinetic energy

So gain in potential energy = 72.72 J

PART C)

So here we can use the formula of potential energy in order to find the maximum height

`U = mgh`

`72.72 = 101(9.81)h`

`h = 0.0735 m`

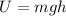
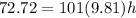
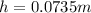
so she will be 7.35 cm above the initial height

PART D)

By energy conservation we can find the final speed when she hit the water

So by energy conservation law we know that

`KE_i + U_i = KE_f`

`72.72 + 101(9.8)6 = (1)/(2)(101)v_f^2`

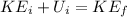
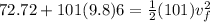
now we have

`v_f^2 = 119.04`

`v_f = 10.91 m/s^2`