Question

Write the following two sequences using summation notation:

5 - 10 + 15 - 20 + 25 - ..... 40
5 - 10 + 15 - 20 + 25 - .....
(Hint: these are different)

Answer 1

Explanation:

Sequence 1:

This is a finite sequence ending with 40

5-10+15-20+...40

= 5(1-2+3-4+5-6+7-8) (by taking 5 as common factor)

This is an alternating series with even numbers in the series having negative sign

Hence can be written as

`\Sigma _(1) ^(8) 5[(-1)^(n-1) (n)`

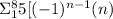
This gives the I sequence in the summation notation. Since there are only 8 terms n can take values as 1 to 8, with odd terms positive.

---------------------------------

Sequence 2:

This is the same as the previous sequence but with end point as infinite

This is an infinite series. Hence n can vary from 1 to infinity.

Thus sum would be

`\Sigma _(1) ^(\infty ) 5[(-1)^(n-1) (n)`

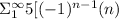
(Note that only the ending number is difference for both.)