Question

The rules for license plates in Idaho are 3 letters followed by 4 numbers (example ABC 1234), where the first letter can only be the letters I, D, A, H, or O. How many different license plates can there be? In what way can Idaho increase the number of license plates?

a. 26 x 26 x 26 x 10 x 10 x 10 x 10 – Use vowels and numbers.

b. 26 x 25 x 24 x 10 x 9 x 8 x 7- keep I, D, A, H, O as the first letter

c. 24 x 25 x 26 x 7 x 8 x 9 x 10 – use 3 letters and 3 numbers

d. 5 x 26 x 26 x 10 x 10 x 10 x 10 – Allow for more first letters to be used.

Answer 1

The correct answer is option d.

Explanation:

The rules for license plates in Idaho are 3 letters followed by 4 numbers (example ABC 1234), where the first letter can only be the letters I, D, A, H, or O.

(I/ D/ A/ H/ O) ,a, a , n ,n, n, n

a = Any alphabet from 'a' to 'z'.

n = any number for 0 to 9.

Total numbers alphabets that can be used at first place = 5

Total number of alphabets = 26

Total number of numeral i.e 0 to 9 = 10

Since repetitions of alphabets and numbers are allowed.Then number of different number plates possible with this format:

`5* 26* 26* 10* 10* 10* 10=33,800,000`

Idaho increase the number of license plates by using any of alphabets from the 26 alphabets.

`26* 26* 26* 10* 10* 10* 10=175,760,000`

Answer 2

Option d

Explanation:

We can solve this problem using the mathematical principles of permutations.
`P(n,r) = (n!)/((n-r)!)`

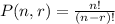
Where n is the number of things to choose and you choose r from them

To begin we must clarify that the English alphabet has 26 letters and there are 10 possible digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Imagine then a plate that contains 6 characters. Three letters and three numbers.

{A, B, C, 1, 2, 3}

The first character can only be 1 of the following 5 letters I, D, A, H or O.

So:

`P(5,1) = (5!)/((5-1)!) = 5`

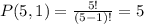
The next two characters can be any of the 26 letters of the alphabet.

`P(26,1) = (26!)/((26-1)!) = 26`

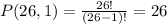
The last 3 characters can be any of the 10 numbers mentioned above.

`P(10,1) = (10!)/((10-1)!) = 10`

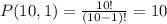
Therefore, the number of possible permutations is:

{5x26x26x10x10x10} = 3380000

To increase this number should allow the use of any of the 26 letters in the first character of the plate

{26x26x26x10x10x10} = 17576000

The correct answer is option d.

d. 5 x 26 x 26 x 10 x 10 x 10 x 10 – Allow for more first letters to be used.