Question

What is the value of x

Answer 1

`x=(160-51)/(2) =54.5`

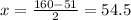
Explanation:

"Theorem 9-13: The measure of an angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside the circle is equal to half the difference of the measures of the intercepted arcs."

Basically no matter what other circle, secant or tangent you get, you just use the formula
`Outer\angle=(far.point - near.point)/(2)`

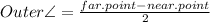
If you need the outer angle, just put the other angles in and solve

If you need the far or near point angle, re-arrange the formula to get that value.

Answer 2

The value of x is 58.

Explanation:

According to the angle of Intersecting Secants Theorem, the angle of intersection of secants is equal to half of difference of major and minor arc.

`\text{Angle of intersection of secants}=(1)/(2)(\text{Major arc - Minor arc})`

`\text{Angle of intersection of secants}=(1)/(2)(\text{Major arc - Minor arc})`

From the given figure it is clear that the angle of intersection of secants is 51, major axis is 160° and minor axis is x°.

`51=(1)/(2)(160-x)`

Multiply both sides by 2.

`51* 2=(1)/(2)(160-x)* 2`

`102=160-x`

Add x on both the sides.

`102+x=160`

Subtract 102 from both the sides.

`x=160-102`

`x=58`

Therefore value of x is 58.