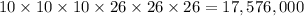Question

The format for automobile license plates in Georgia before 2000 was 3 numbers followed by 3 letters (example: 123 ABC). How many different license plates in this format can there be? Which is the correct setup to solve?

a. 9 x 9 x 10 x 25 x 24 x 25

b. 26 x 26 x 26 x 10 x 10 10

c. 25 x 25 x 26 x 9 x 9 x 10

d. 10 x 10 x 26 x 26 x 26 x 26

Answer 1

It should be b because 3 numbers each has 10 possibilities, and the letters each has 26 possibilities.

Answer 2

The correct answer is option c.

Explanation:

The format for automobile license plates in Georgia before 2000 was 3 numbers followed by 3 letters .

n ,n, n, a ,a, a

a = Any alphabet from 'a' to 'z'.

n = any number for 0 to 9.

Total number of alphabets = 26

Total number of numeral i.e 0 to 9 = 10

Since repetitions of alphabets and numbers are allowed.Then number of different number plates possible with this format:

`10* 10* 10* 26* 26* 26=17,576,000`