Question

Consider the function and its inverse, . Which statement describes how the x-intercept for the original function can be determined? The x-intercept for f(x) is the constant in the f(x) equation. The x-intercept for f(x) is the constant in the f–1(x) equation. The x-intercept for f(x) is the reciprocal of the constant in the f(x) equation. The x-intercept for f(x) is the reciprocal of the constant in the f–1(x) equation.

Answer 1

Answer: B

The x-intercept for f(x) is the constant in the f–1(x) equation.

Explanation:

Answer 2

The x-intercept for f(x) is the constant in the f–1(x) equation.

Explanation:

The x-intercept refers to the point where the graph of a function crosses the x-axis. At this point, the value of y is usually zero.

Consider a function;

`f(x)=2x+3`

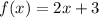
The x-intercept of this function is determined by replacing f(x) with 0 and solving for x. For this function the x-intercept is;

`-(3)/(2)`.

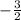Now, the inverse of the function is evaluated by substituting f(x) with x and x with y in the original function and then solve for y;

`x=2y+3`

`y=(x)/(2)-(3)/(2)`

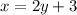
Clearly, The x-intercept for f(x) is the constant in the f–1(x) equation.