Question

What is the equation of the graph below?

Answer 1

Answer:A

Explanation:

look at the graph and u will find the same answer

Answer 2

Answer: The correct option is (A)
`y=\sin(x+90^\circ).`

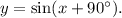
Step-by-step explanation: We are to select the correct equation of the given graph.

From the graph, we can see that

y (x = 0) = 1,

y (x = 90°) = 0,

y (x = -90°) = 0,

y (x = 180°) = -1,

y (x = -180°) = -1, etc.

Option (A) is

`y=\sin(x+90^\circ).`

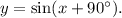
We have

`y(x=0)=\sin(0+90^\circ)=\sin90^\circ=1,\\\\y(x=90^\circ)=\sin(90^\circ+90^\circ)=\cos90^\circ=0,\\\\y(x=-90^\circ)=\sin(-90^\circ+90^\circ)=\sin0^\circ=0,\\\\y(x=180^\circ)=\sin(180^\circ+90^\circ)=-\sin90^\circ=-1,\\\\y(x=-180^\circ)=\sin(-180^\circ+90^\circ)=-\sin90^\circ=-1,~etc.`

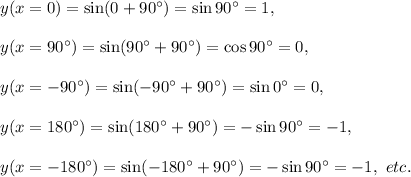
So, this option is correct.

Option (B) is

`y=\cos(x+90^\circ).`

We have

`y(x=0)=\cos(0+90^\circ)=\cos90^\circ=0\\eq 1.`

So, this option is not correct.

Option (C) is

`y=\sin(x+45^\circ).`

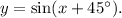
We have

`y(x=0)=\sin(0+45^\circ)=\sin45^\circ=(1)/(\sqrt2)\\eq 1.`

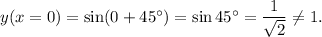
So, this option is not correct.

Option (D) is
`y=\sin(x+90^\circ).`

`y=\cos(x+45^\circ).`

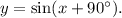
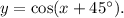
We have

`y(x=0)=\cos(0+45^\circ)=\cos45^\circ=(1)/(\sqrt2)\\eq 1.`

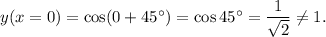
So, this option is also not correct.

Thus, the correct option is (A)