Question

Which description compares the domains of function A and Function B correctly?

Function A f(x) = log x
Function B
A - the domain of function A is the set of real numbers greater than or equal to 1
The domain of function B is the set of real numbers greater than 1
B- the domain of function A is the set of real numbers is greater than 0
The domain of the function B is the set of real numbers greater than or equal to 1
C- the domain of both functions is the set of real numbers
D- the domain of both functions is the set of real numbers greater than or equal to 1

Answer 1

Choice B is correct; the domain of function A is the set of real numbers greater than 0

The domain of the function B is the set of real numbers greater than or equal to 1

Explanation:

The domain of a function refers to the set of x-values for which the function is real and defined. The graph of function B reveals that the function is defined when x is equal 1 and beyond; that is its domain is the set of real numbers greater than or equal to 1 written in interval notation as;

`[1, infinity)`

On the other hand, the natural logarithm function is defined everywhere on the real line except when x =0; this will imply that its domain is the set of real numbers greater than 0 . In fact, the y-axis or the line x =0 is a vertical asymptote of the natural log function; meaning that its graph approaches this line indefinitely but neither touches nor crosses it.

Answer 2

B- the domain of function A is the set of real numbers is greater than 0

The domain of the function B is the set of real numbers greater than or equal to 1

Explanation:

The function A is
`f(x) = log(x)`

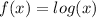
By definition we know that the function
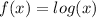`f(x) = log(x)` is not defined for values of
`x\leq0`

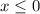
Therefore the domain of
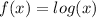`f(x) = log(x)` is:

All real numbers greater than 0.

`x> 0`

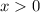
Function B shown in the graph is a curve that goes in x from x = 1 to infinity.

Therefore it can be seen that the domain of this function is:

all real numbers greater than or equal to 1.

`x\geq 1`.

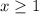Therefore the correct option is B.