Question

A NASA centrifuse spins astronauts around in a compartment attached to a long arm. A diagrem of the centrifuge is shown below.

a. draw and label the direction of the velocity vector on the picture.

b. Draw and label the direction of the centripetal acceleration vector on the picture.

c. If the arm has a radius of 7.1 m and spins the astronaut with a speed of 13.5 m/s, what is the acceleration of the astronaut?

d. The maximum acceleration the centrifuge can produce is 14.5 g/ What is the acceleration in
`m/s^(2)`

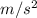
e. How fast would the compartment have to move to produce an acceleration of 14.5 g?

Answer 1

a) The velocity vector is always perpendicular to the radius of the circle

b) Since centripetal acceleration makes the velocity vector rotate, a.cent is directed to the center of the circle along its radius.

c) a=v^2/R=13.5^2/7.1=25.67 m/s/s

d) a.max=14.5*9.8=142.1 m/s/s

e)
`v=√(a.max*R)=√(142.1*7.1)=31.76` m/s

Answer 2

Your diagram probably shows a picture of a circle.

a. The velocity vector points in a direction that is always tangent to the circle.

b. The acceleration vector points toward the center of the circle.

c. In uniform circular motion, we have

`a=\frac{v^2}r=(\left(13.5\,(\rm m)/(\rm s)\right)^2)/(7.1\,\rm m)=25.7\,(\rm m)/(\mathrm s^2)`

d. With
`g=9.80\,(\rm m)/(\mathrm s^2)`, we have

`14.5g=142\,(\rm m)/(\mathrm s^2)`

e. The required velocity
`v` satisfies

`14.5g=(v^2)/(7.1\,\rm m)\implies v=√(102.95g)=31.8\,(\rm m)/(\rm s)`