Answer:
(a) 1
(b) 1
(c) 3.03
Explanation:
The given quadratic equation is
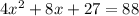
Subtract 27 from both sides.
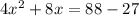
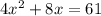
Taking out common factor.
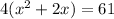
Divide both sides by 4.
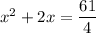
If an expression is
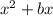 , then we need to add
, then we need to add
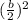 , to make it perfect square.
, to make it perfect square.
Here, b=2, so
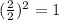
Add 1 on both sides.
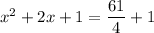
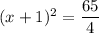
Taking square root on both sides.
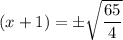
Subtract 1 from both sides.
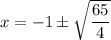
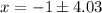
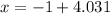 and
and
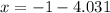
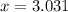 and
and
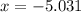
Only one solution is positive.
Greatest solution is 3.031, therefore the approximate value of this solution is 3.03.