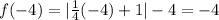Question

Write an equation of the translated function of the parent function f(x)=|x| with the following transformations:

Horizontal stretch of a factor of 4 and a vertex of (-4,-4). Assume that the x and y axis increase in increments of 2

Answer 1

Option b

Explanation:

To write the searched equation we must modify the function f (x) = | x | in the following way:

1. Do y = f(x + 4)

This operation horizontally shifts the function f(x) = | x | by a factor of 4 units to the left on the x axis.

y = | x +4 |

2. Do
`y = f ((1)/(4)x)`

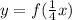
This operation horizontally expands the function f (x) = | x | in a factor of 4 units.
`y = |(1)/(4)x + 1|`

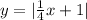
3. Do
`y = f(x)-4`

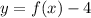
This operation vertically shifts the function f (x) = | x | by a factor of 4 units down on the y-axis.

`y = |(1)/(4)x +1| -4`

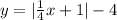
4. After these transformations the function f(x) = | x | it looks like:

`f(x) = |(1)/(4)x +1| -4`

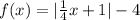
Therefore the correct option is option b. You can verify that your vertex is at point (-4, -4) by making f (-4)

`f(-4) = |(1)/(4)(-4) +1| -4 = -4`