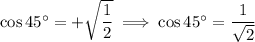It's a value you should probably memorize:
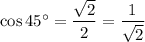
You can derive it using some trigonometric identities, other known values of cosine, and properties of the cosine function. For example, using the double angle identity for cosine:
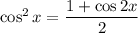
If
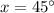 , then
, then
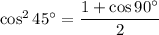
and you probably know that
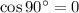 , so
, so

When we take the square root, we should take the positive root because
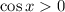 whenever
whenever
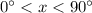 :
: