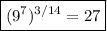Answer:
27.
Explanation:
It is one property of exponents that for any numbers a, b, and c
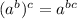
Therefore, using this property the expression
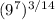 becomes
becomes
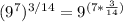 .
.
and when when simplify the exponents, we get:
 .
.
Since for any number
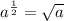 (
(
 in the exponent means the square root) ,
in the exponent means the square root) ,
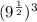 is rewritten as
is rewritten as
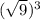
which simplifies to
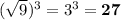
Thus,