Answer:
Option C.
Explanation:
Let
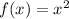 be a quadratic function
be a quadratic function
Then we do the function
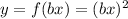
Where b is a real number.
If
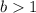 then the function
then the function
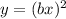 represents a horizontal compression of the function
represents a horizontal compression of the function
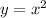
If
 Then the function
Then the function
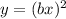 represents a horizontal expansion compression of the function
represents a horizontal expansion compression of the function
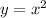 by a factor of
by a factor of
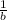
In this case, the equation is:
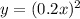 Then:
Then:
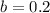

Thus
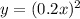 is a horizontal expansion of the function
is a horizontal expansion of the function
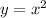 by a factor of
by a factor of
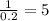 .
.
The correct option is: Option C