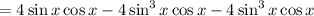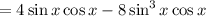If you have some knowledge of complex numbers: This follows pretty much immediately from Euler's formula and DeMoivre's theorem,
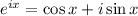 (Euler)
(Euler)
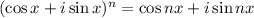 (DeMoivre)
(DeMoivre)
so that
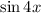 is the imaginary part of the expanded left hand side.
is the imaginary part of the expanded left hand side.
If that's unfamiliar to you, you can make use of several identities to expand
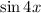 :
:
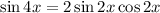 (double angle sine)
(double angle sine)
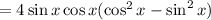 (double angle sine and cosine)
(double angle sine and cosine)
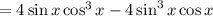
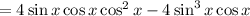
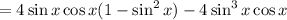 (Pythagorean)
(Pythagorean)