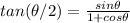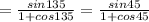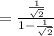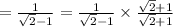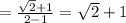Question

I need help with this problem if someone could be of assistance

Answer 1

1) cos 105°

2) tan 67.5°

3) sin 67.5°

4) tan 165°

Explanation:

From half angle identity

`sin(\theta )/(2)= \sqrt{(1-cos\theta )/(2)}`

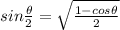
For sin 67.5 = sin (135/2)

Here 67.5° lies in Ist quadrant therefore

`sin(\theta )/(2)= \sqrt{(1-cos\theta )/(2)}`

`=\sqrt{((1-cos135))/(2)}=\sqrt{(1+cos45)/(2)}`

`=\sqrt{(1+(1)/(√(2)))/(2)}=\sqrt{(√(2)+1)/(2√(2))}`

`=\sqrt{((√(2)+1)(√(2)))/(2√(2)* √(2))}`

`=\sqrt{(√(2)+2)/(2)}=\frac{\sqrt{√(2)+2}}{2}`

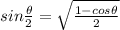
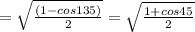
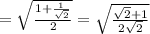
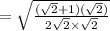
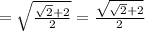
For cos 105 = cos (210/2)

From half angle identity

`cos(\theta/2) =\pm \sqrt{(1+cos\theta )/(2)}`

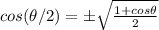
Since cos 105 lies in second quadrant

Therefore
`cos(\theta/2) =-\sqrt{(1+cos\theta )/(2)}`

`cos(\210/2) =-\sqrt{(1+cos210)/(2)}`

`=-\sqrt{(1-cos60)/(2)}=-\sqrt{(1-(√(3))/(2))/(2)}`

`=-\sqrt{(2-√(3))/(4)}=-\frac{\sqrt{2-√(3)}}{2}`

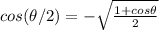
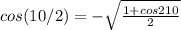
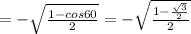
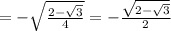
For tan165 = tan (330/2)

From half angle identity

`tan(\theta/2) =(sin\theta )/(1+cos\theta )`

`=(sin330)/(1+cos330)=-(sin30)/(1+cos30)`

`=-((1)/(2))/(1+(√(3))/(2))=-(1)/(2+√(3))`

`=-(2-√(3))/((2+√(3))(2-√(3)))=-(2-√(3))/(4-3)=-(2-√(3))=√(3)-2`

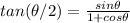
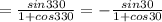
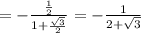
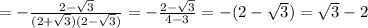
For tan 67.5 = tan (135/2)

From half angle identity

`tan(\theta/2) =(sin\theta )/(1+cos\theta )`

`=(sin135)/(1+cos135)=(sin45)/(1+cos45)`

`=((1)/(√(2)))/(1-(1)/(√(2)))`

`=(1)/(√(2)-1)=(1)/(√(2)-1)* (√(2)+1)/(√(2)+1)`

`=(√(2)+1)/(2-1)=√(2)+1`