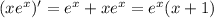Question

Use first principle to find y'all for y=xe^x

Answer 1

By definition of the derivative,

`y'=\displaystyle\lim_(h\to0)\frac{(x+h)e^(x+h)-xe^x}h`

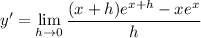
We can employ the standard manipulation for proving the product rule:

`\displaystyle\lim_(h\to0)\frac{(x+h)e^(x+h)-xe^(x+h)+xe^(x+h)-xe^x}h`

`\displaystyle\lim_(h\to0)\frac{(x+h)e^(x+h)-xe^(x+h)}h+xe^x\lim_(h\to0)\frac{e^h-1}h`

`\displaystyle\lim_(h\to0)e^(x+h)\lim_(h\to0)\frac{(x+h)-x}h+xe^x\lim_(h\to0)\frac{e^h-1}h`

`e^(x+0)\displaystyle\lim_(h\to0)\frac hh+xe^x\lim_(h\to0)\frac{e^h-1}h`

`e^x+xe^x\displaystyle\lim_(h\to0)\frac{e^h-1}h`

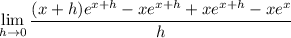
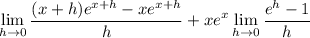
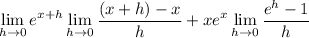
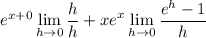
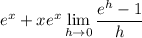
The remaining limit is pretty well-known and has a value of 1. We can derive it from the definition of
`e`,

`e=\displaystyle\lim_(n\to0)(1+n)^(1/n)`

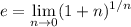
In the limit above, we substitute
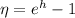`\eta=e^h-1`, so that
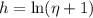`h=\ln(\eta+1)`. As
`h\to0`, we have
`\eta\to e^0-1=0`:

`\displaystyle\lim_(h\to0)\frac{e^h-1}h=\lim_(\eta\to0)\frac\eta{\ln(\eta+1)}`

`\displaystyle=\lim_(\eta\to0)\frac1{\frac1\eta\ln(\eta+1)}`

`\displaystyle=\frac1{\lim\limits_(\eta\to0)\ln(\eta+1)^(1/\eta)}`

`\displaystyle=\frac1{\ln\left(\lim\limits_(\eta\to0)(\eta+1)^(1/\eta)\right)}`

`=\frac1{\ln e}=\frac11=1`

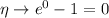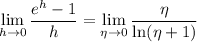
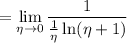
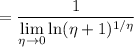
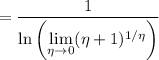
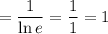
After all this, we've shown that

`(xe^x)'=e^x+xe^x=e^x(x+1)`