Question

URGENT, HELP ASAP

Sales of a popular toy were about 20 million in 2000 and growing by about 5% each year. At this growth rate, the function f(x) = 20(1.05)x gives the annual number of toys sold in millions in the xth year after 2000. Using this model, in about what year will the annual sales surpass 37 million?


A 2010
B 2020
C 2015
D 2013

Answer 1

The sales will surpass 37 million in about 2013.

Explanation:

The answer can be found via solving an exponential inequality as follows:

`f(x) = 20(1.05)^x\\20(1.05)^x> 37\\1.05^x> (37)/(20)\\x\log 1.05>\log(37)/(20)=\log 37 - \log 20\\x>(\log 37 - \log 20)/\log 1.05=12.6\\x>12.6 \,\,\mbox{years}`

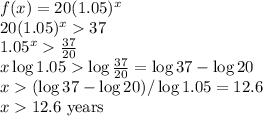
Any number of years larger than 12.6 will satisfy the inequality, i.e., after more than 12.6 years from year 2000, the annual sales will surpass 37 million. The answer to the exact question will then be: in about 2013 the sales will surpass 37 million.