Question

Help!!! Asap

Which of the following lines would be parallel to y = 2x -4. (Select ALL that apply.

A. A line passing through points (0,6) and (2,2).

B. A line passing through points (1,10) and (0,8).

C. A line passing through points (10,1) and (8,0).

D. A line passing through points (4,2) and (8,10).

Answer 1

Answer: The answers are

A line passing through points (1,10) and (0,8)

A line passing through points (4,2) and (8,10)

Explanation:

Just took the test and got an A<3

Answer 2

option B A line passing through points (1,10) and (0,8)

option D A line passing through points (4,2) and (8,10)

Explanation:

we know that

If two lines are parallel , then their slopes are the same

In this problem we have

`y=2x-4`

The slope is equal to

`m=2`

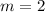
Remember that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

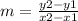
Verify each case

case A) A line passing through points (0,6) and (2,2)

substitute in the formula

`m=(2-6)/(2-0)`

`m=(-4)/(2)`

`m=-2`

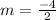
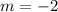
Compare with the slope of the given line (m=2)

`-2\\eq2`

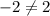
therefore

This line is not parallel to the given line

case B) A line passing through points (1,10) and (0,8)

substitute in the formula

`m=(8-10)/(0-1)`

`m=(-2)/(-1)`

`m=2`

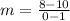
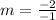
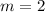
Compare with the slope of the given line (m=2)

`2=2`

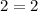
therefore

This line is parallel to the given line

case C) A line passing through points (10,1) and (8,0)

substitute in the formula

`m=(0-1)/(8-10)`

`m=(-1)/(-2)`

`m=0.5`

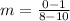
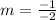
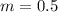
Compare with the slope of the given line (m=2)

`0.5\\eq2`

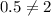
therefore

This line is not parallel to the given line

case D) A line passing through points (4,2) and (8,10)

substitute in the formula

`m=(10-2)/(8-4)`

`m=(8)/(4)`

`m=2`

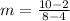
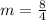
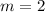
Compare with the slope of the given line (m=2)

`2=2`

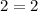
therefore

This line is parallel to the given line