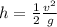Question

Learning Goal: To apply the law of conservation of energy to an object launched upward in the gravitational field of the earth. In the absence of nonconservative forces such as friction and air resistance, the total mechanical energy in a closed system is conserved. This is one particular case of the law of conservation of energy. In this problem, you will apply the law of conservation of energy to different objects launched from the earth. The energy transformations that take place involve the object's kinetic energy K=(1/2)mv2 and its gravitational potential energy U=mgh. The law of conservation of energy for such cases implies that the sum of the object's kinetic energy and potential energy does not change with time. This idea can be expressed by the equation Ki+Ui=Kf+Uf , where "i" denotes the "initial" moment and "f" denotes the "final" moment. Since any two moments will work, the choice of the moments to consider is, technically, up to you. That choice, though, is usually suggested by the question posed in the problem. Using conservation of energy, find the maximum height h_max to which the object will rise

Answer 1

`h=(1)/(2)(v^2)/(g)`

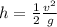
Step-by-step explanation:

Let's assume that an object is launched straight upward in a gravitational field. Its initial kinetic energy is given by

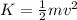`K=(1)/(2)mv^2` (1)

where m is the mass and v is the initial speed.

As the object goes higher, its kinetic energy decreases and it is converted into gravitational potential energy, since the total mechanical energy (sum of kinetic and potential energy) must remain constant:

`E=K+U=const.`

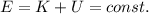
At the highest point of the trajectory, the speed of the object is zero (v=0), so the kinetic energy is also zero (K=0), which means that all the kinetic energy has been converted into potential energy:

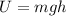`U=mgh` (2)

where g is the gravitational acceleration and h is the maximum height of the object.

Due to conservation of energy, we can write that (1) and (2) are equal, so:

`(1)/(2)mv^2=mgh`

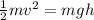
from which we can derive an expression for the maximum height reached by the object

`h=(1)/(2)(v^2)/(g)`