Answer:
Hence, the average rate of change is:

Explanation:
We are asked to calculate the average value of the function:
 in 2 ≤ x ≤ 6
in 2 ≤ x ≤ 6
The average rate of change of the function f(x) in the interval 2 ≤ x ≤ 6 is given as:
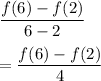
Now,
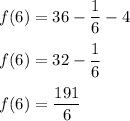
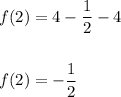
Hence, the average rate of change is:
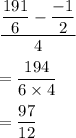
Hence, the average rate of change is:
